
Trích 550 Câu Đồ Thị Giải Có Lời Chi Tiết Sóng Cơ Dạng 2 Sóng Dừng | Blog Góc Vật Lí
Thí nghiệm hiện tượng sóng dừng trên sợi dây đàn hồi có chiều dài L và một đầu cố định, một đầu tự do. Kích thích sợi dây dao động bằng tần số f thì khi xảy ra hiện tượng sóng dừng trên sợi dây hình thành các bó sóng. Đồ thị biểu diễn mối quan hệ giữa tần số f và số bụng sóng trên dây như hình bên. Giá trị của y là
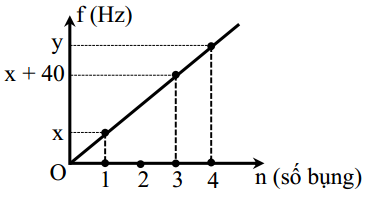
A.40 Hz
B.60 Hz
C.70 Hz
D.80 Hz
Hướng giải:
Điều kiện có sóng dừng L = (2k + 1)4 = (2k + 1)v4f
+ Với n = 1 → k = 0 → L = v4x (1)
+ Với n = 3 → k = 2 → L = 5v4(x+40) (2)
Giải (1) và (2) → x = 10 Hz → L = v40
+ Với n = 4 → k = 3 → L = 7v4y→ y = 7v4L = 70 Hz 👉 C
Một sóng dừng trên sợi dây hai đầu cố định. Ở thời điểm t, hình ảnh sợi dây (như hình vẽ). Biết tốc độ dao động của điểm bụng bằng 3π% tốc độ truyền sóng. Biên độ dao động của điểm bụng là
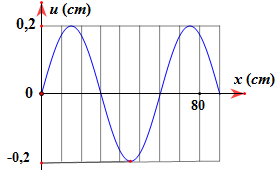
A.0,2 cm B.0,9 cm
C.0,15 cm D.0,4 cm
Hướng giải:
Từ đồ thị ta tính được λ = 60 cm
Theo đề ta có: Ab.2πfλf = 3π% → Ab = 90% = 0,9 cm 👉 B
Trên một sợi dây đàn hồi OB với hai đầu cố định đang có sóng dừng với tần số f xác định (2,4 Hz < f < 2,6 Hz), sóng tới tại B có biên độ là 3 cm. Tại thời điểm t1 và thời điểm t2 = t1 + 6,9 s, hình ảnh sợi dây đều có dạng như hình vẽ. Số lần sợi dây đã duỗi thẳng từ thời điểm t1 đến thời điểm t2 là

A. 32 lần B. 33 lần
C. 34 lần D. 35 lần
Hướng giải:
Chọn gốc thời gian t1 = 0
Vì tại hai thời điểm t1 và t2 hình ảnh dây trùng nhau → trạng thái lặp lại ⇒ t2 = nT = nf = 6,9 s (với n nguyên) ⇒ f = n6,9
Kết hợp với dữ kiện của đề → 2,4<n6,9< 2,6
⇒ 16,56< n < 17,94 ⇒ Chọn n = 17.
Trong 1 chu kì có 2 lần dây duỗi thẳng → trong 17 chu kì có 34 lần duỗi thẳng dây 👉 C
Cho một sợi dây cao su căng ngang. Làm cho đầu O của dây dao động theo phương thẳng đứng. Hình vẽ mô tả hình dạng sợi dây tại thời điểm t1 (đường qua O) và t2=t1+0,2 s (đường không qua O). Tại thời điểm t3=t2+215s thì độ lớn li độ của phần tử M cách đầu dây một đoạn 2,4 m (tính theo phương truyền sóng) là3 cm. Gọi δ là tỉ số của tốc độ cực đại của phần tử trên dây với tốc độ truyền sóng. Giá trị của δ gần giá trị nào nhất sau đây?
A.0,0025. B.0,022. C.0,012. D.0,018.
Hướng giải:
Từ đồ thị ta thấy λ = 6,4 m
Từ thời điểm t1 đến thời điểm t2 sóng truyền được quãng đường S = 7,2 – 6,4 = 0,8 m theo phương Ox
→ Vận tốc truyền sóng v = St=0,80,2 = 4 m/s
Trong 1 chu kì thì λ ~ T →0,86,4=0,2T→ T = 1,6 s
Chọn gốc thời gian tại thời điểm t1→ Phương trình sóng có dạng u = Acos(5π4t +2)
→ Phương trình sóng tại M có dạng uM = Acos(5π4t +2 - 2πx)
Tại t3 = t2 + 215 = 13s thì uM = 3 cm →3 = Acos(5π4.13 + 2 - 2π.2,46,4) = Acos6→ A = 2 cm
Vậy δ = A.2πTT=A.2π = 0,019 👉 D
Một sóng cơ truyền theo tia Ox trên một sợi dây đàn hồi rất dài với chu kì 6 s. Hình vẽ bên là hình ảnh sợi dây ở các thời điểm t0 và t1. Nếu d1d2=57 thì tốc độ của điểm M ở thời điểm t2 = t1 + 4,25 s là

A.4π3mm/s B.2π3mm/s
C.4π3mm/s D.4π23mm/s
Hướng giải
Từ đồ thị ta thấy d1 + d2 = λ; kết hợp với d1d2=57→ d2 = 712λ và d1 = 512λ tương ứng t = 5T12→ ∆φ = 5π6

Biểu diễn li độ M trên vòng tròn lượng giác ta tính được pha ban đầu của M: φ = - 5π12
→ Phương trình sóng tại M: u = 8cos(3t - 5π12) mm
→ Tốc độ của M tại thời điểm t2 = t1 + 4,25 = 6,75 s: v = u’≈ 4,2 mm/s 👉 A
Một sóng hình sin đang truyền trên một sợi dây theo chiều dương của trục Ox. Hình vẽ mô tả hình dạng của sợi dây tại thời điểm t1 và t2 = t1 + 0,3 s. Chu kì sóng là

A.0,9 s B.0,4 s
C.0,6 s D.0,8 s
Hướng giải:
Từ đồ thị ta tính được λ = 8 ô
Từ thời điểm t1 đến thời điểm t2 sóng truyền được quãng được 3 ô, tương ứng 3T8 = 0,3 s
→ T = 0,8 s👉 D
Một sợi dây căng ngang đang có sóng dừng với bước sóng λ, đồ thị biểu diễn hình ảnh dây ứng với hai thời điểm t1 (đứt) và t2 (liền). Biết tại thời điểm t1 phần tử B đang có li độ bằng biên độ của phần tử M, tìm khoảng cách MB gần đáp án.
A. 0,19λ B. 0,20λ
C. 0,192λ D. 0,21λ
Hướng giải:
Biên độ sóng tại M: AM = Abcos2πd hay cos2πd = 13→2πd ≈ 1,231
→ d ≈ 0,1959λ 👉C
{d là khoảng cách từ B đến M trên Ox}

